Heuristics Are Guaranteed to Find an Optimal Solution.
- C: kills(curiosity,tuna)
- constants symbols: jack, curiosity, tuna.
- relation symbols: dog, owns, animal-lover, animal, kills, cat.
- variable symbols: s, u, w, x, y, z.
- (8 points) Translate the axioms and the negation of the conclusion into clausal form. Show each step of the translation (remember that the order in which you apply the steps is crucial). To simplify your life, the translations of A1, and A2 into clausal form are already provided below. Note that in order to translate A1 into clausal form, a new constant called spot has been introduced in order to eliminate the existential quantifier.
- A1.1: dog(spot)
- A1.2: owns(jack,spot)
- A2: !dog(y) || !owns(x,y) || animal-lover(x)
- A3: !animal-lover(w) || !animal(s) || !kills(w,s)
- A4: kills(jack,tuna) || kills(curiosity,tuna)
- A5: cat(tuna)
- A6: !cat(u) || animal(u)
- !C: !kills(curiosity,tuna)
- (17 points) Apply resolution (state explicitly what clauses are resolved and which substitutions are made) until the empty clause is found.
!C: !kills( curiosity, tuna ) A4: kills( jack, tuna ) || kills( curiosity, tuna )
A7: kills( jack, tuna) A3: !animal-lover( w ) || !animal( s ) || !kills ( w, s )
w <- jack s <- tuna A8: !animal-lover( jack ) || !animal( tuna ) A6: !cat( u ) || animal( u )
u <-tuna A9: !animal-lover( jack) || !cat( tuna ) A5: cat( tuna )
A10: !animal-lover( jack ) A3: !Dog( y ) || !Owns( x, y ) || animal-lover( x )
A11: !Dog( y ) || !Owns( jack, y) A1.2: Owns( jack, Spot )
A12: !Dog( Spot ) A1.1: Dog( Spot )
A13:Success! Hence Curiosity Killed the Cat!!!
Problem IV. Search (25 points)
Suppose that you need to find a path between S and G in the following graph. The number attached to each edge in the graph represents the COST of traversing the edge. 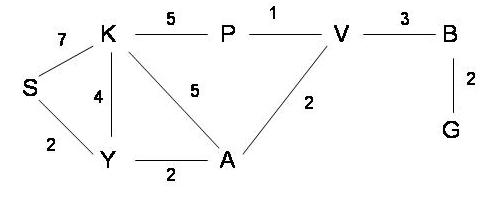
Assume also that the ESTIMATED distances to the goal are given by the following table:
| Node: | S | K | Y | A | P | V | B | G | |||||||||
| Estimated Distance to G: | 10 | 4 | 8 | 2 | 4 | 4 | 2 | 0 |
For EACH of the following search methods list the nodes in the order in which they are EXPANDED by the search method while looking for a solution. Also, show the search tree as it is constructed by the search method. When everything else is equal, order the nodes in alphabetical order.
- (7 points) Branch-and-Bound WITH Dynamic Programming
Branch and Bound works by expanding the head of the queue, and then sorting by least cost-so-far. Costs at nodes appear next to the letter. Dynamic Programming refers to the removal of nodes that are the same letter as another node but with a higher cost-so-far. These are marked by an X in the tree.List of expanded nodes: S Y A K V P B G
Search Tree:
/ \ / \ K-7 Y-2 X / \ / \ A-4 K-6 / | | \ / | | \ K-9 V-6 A-11 P-11 X / \ X X / \ B-9 P-7 | | | | G-11 K-12 X
- (6 points) A*
A* works by expanding the head of the queue, and then sorting by least cost-so-far plus heuristic. Cost+Heuristic at nodes appears next to the letter.List of expanded nodes: S Y A K V B G
Search Tree:
S / \ / \ K-11 Y-10 / \ / \ A-6 K-10 / | | \ / | | \ K-13 V-10 A-13 P-15 / \ / \ B-11 P-11 | | G-11
- (6 points) Greedy Search (= Best 1st Search)
Greedy Search works by expanding the head of the queue, and then sorting by heuristic. Heuristics at nodes appear next to the letter.List of expanded nodes: S K A P V B G or S K A P V A B G
Search Tree(s):
S . S / \ . / \ / \ . / \ K-4 Y-8 . K-4 Y-8 / | \ . / | \ / | \ . / | \ A-2 Y-8 P-4 . A-2 Y-8 P-4 / | | . / | | / | | . / | | Y-8 V-4 V-4 . Y-8 V-4 V-4 / \ . / \ / \ . / \ P-4 B-2 . A-2 B-2 | . | | G-0 . Y-8 G-0
- (6 points) Hill-climbing
Hill Climbing works by expanding the head of the queue, sorting the children by heuristic, and placing those sorted children into the queue. Heuristics at nodes appear next to the letter.List of expanded nodes: S K A V B G
Search Tree:
S / \ / \ K-4 Y-8 / | \ / | \ A-2 Y-8 P-4 / | / | / \ / \ P-4 B-2 | | G-0
EXTRA CREDIT Problem. Planning (10 points)
Given- an initial state,
- a desired goal state,
- a collection of operators to transform states into other states, each operator having preconditions and postconditions
- (2 points)Describe what a plan (to go from the initial state to the goal state) is.
A plan is a (partially) ordered collection of operators that, when applied in the order specified, tranform the initial state into the goal state.
- (8 points) Describe how to construct a plan.
Outline the overall process, explaining in particular (1)how the search for the plan is conducted, (2) when an operator is added to the plan, (3) what a threat is and how it is resolved, and (4) when the search ends.(1) A plan is constructed using "backward chaining" starting from the goal state and finding operators whose postconditions match the assertions in the goal state, and then the process is applied recursively to satisfy the preconditions of those operators. (2) An operator is introduced when there is an assertion in the goal state or a precondition in any of the operators currently in the plan that is still not satified by other operators in the plan or the assertions in the initial state. If there are several operators that can be introduced to satisfy such assertion or precondition, then those operators are explored in a depth-1st manner (with backtracking). (3) When the postcondition of an operator 1 in the plan matches/satisfies the precondition of another operator 2 in the plan, we say that operator 1 "establishes" operator 2. A "threatening" situation is present when the postcondition of a third operator in the plan invalidates the precondition of operator 2 that operator 1 has established. A way to resolve this conflict is to add time constraints to the plan, requiring that operators 1 and 2 be executed before operator 3, or that operator 3 be executed before operators 1 and 2. If both options are impossible to satisfy, then the current branch of the search fails and the whole process backtracks. (4) The search for a plan ends successfully when all the assertions in the goal state as well as all preconditions of the operators in the plan are satisfied. The search for a plan ends unsuccessfully when the search has backtracked to the end and there are no more ways to combine the operators to satisfy all conditions.
Heuristics Are Guaranteed to Find an Optimal Solution.
Source: https://web.cs.wpi.edu/~cs4341/C02/Exams/solutions_exam1_c02.html